4.12.2010
from Einstein
Make everything as simple as possible, but not simpler.
- Albert Einstein
The Concept of Innovation is
"Amalgamate organically
Agriculture, Forestry,Fishery,Industry,Science,Arts and Civic Life etc."
Is this neutral?
Is this the Global Justice?
Art Harbour Asia Hub Managers
---Wiki
ムーアの法則（Moore's Law、ムーアのほうそく）は、コンピュータ製造業における歴史的な長期傾向について論じた1つの指標であり、経験則、将来予測である。米インテル社の共同創業者であるゴードン・ムーアが1965年に自らの論文上に示したのが最初であり、その後、半導体業界やコンピュータ産業界を中心に広まった。
ムーアの元々の文章は以下の論文に見られる。
「部品あたりのコストが最小になるような複雑さは、毎年およそ2倍の割合で増大してきた。短期的には、この増加率が上昇しないまでも、現状を維持することは確実である。より長期的には、増加率はやや不確実であるとはいえ、少なくとも今後10年間ほぼ一定の率を保てないと信ずべき理由は無い。すなわち、1975年までには、最小コストで得られる集積回路の部品数は65,000に達するであろう。私は、それほどにも大規模な回路が1個のウェハー上に構築できるようになると信じている。」 "Cramming more components onto integrated circuits", Electronics Magazine 19 April 1965[1]
チップの複雑さはトランジスタの個数に比例すると仮定し、それらが何に使われているかを無視するならば、この法則は今日まで充分時の試練に耐えてきたと言える。しかし、トランジスタ当たりの複雑さは、RAMキャッシュにおいては実行ユニットほど高くないという議論もあり得る。この観点からすれば、ムーアの法則の妥当性は、その定式化のしかたによっては疑問符がつくものとなる。
ゴードン・ムーアのこの将来予測は彼自身によって「法則」と名づけられたわけではなく、カリフォルニア工科大学の教授で、LSI開発などで著名な情報工学者のカーバー・ミードによるものである[1]。
ムーアは今日の機械式マウスの共同発明者であるダグラス・エンゲルバートから、1960年の講義において集積回路のサイズ縮小の見通しについて議論したのを聞いたのかもしれない[2]。1975年には、ムーアは今後2年毎に2倍のペースにしかならないだろうという見通しを立てた。彼は自分が「18ヶ月ごと」と言ったことは一度もないのに、そう引用されたのだと主張している。SEMATECHのロードマップには、24ヶ月ごとのサイクルを辿っている。
公式 [編集]
最も有名な公式は、集積回路上のトランジスタ数[3]は「18ヶ月ごとに倍になる」というものである。1970年代の終わりには、ムーアの法則は最も複雑なチップ上のトランジスタ数の限界として知られるようになった。しかしながら、1チップあたりのコストに対するコンピューティングパワーをどんどん進化させ続けるものとしても、ムーアの法則は引用されるようになった[4]
産業牽引力 [編集]
ムーアの法則は最初は半導体産業での観察と予測によって生まれたが、今日ではより広く受け入れられ、先進的な工業製品一般における性能向上の1つの目標値として用いられることがある。
コンピュータ関係の製品や部品を製造する企業にとって、ムーアの法則が暗示する将来予測は無視できない。例えばCPUやハードディスクのような製品を新規に設計・生産する場合には、最初の出荷まで2年から5年ほどの期間を要するため、こういったメーカーは、投資と収益に関する大きな経済的リスクを負うと共に、数年先の市場を予測した製品開発を行わねばならない。製品の陳腐化が早いいくつかの産業では、先行者利益が大きい分だけ市場参入の遅れは大きな損失を負う可能性があるが、逆に、他社が提供できない新規性があり高性能な製品であっても生産コストが高く販売価格が市場に受け入れられなければ、特殊な用途向きの小さな市場にしか得られない可能性があるため、将来予測は重要である。過去の結果から将来を演繹する将来予測は、それを信じる参加者が多いことでより信頼度の高いものとなり、その1つが「ムーアの法則」といえる。
「18ヶ月ごとに倍になる」という表現は、ムーアの法則が近年の技術の表象的な進み具合をほのめかしている。より短い時間軸で表現されると、ムーアの法則は平均して1週間に1%以上半導体産業全体のパフォーマンスを向上させていると言い換えることができる。
将来のトレンド [編集]
.PNG)
2006年第一四半期において、PCのプロセッサは90nmで製造されており、65nmのチップはIntel(Pentium DおよびIntel Core)からのみ出荷されていた。10年前では、チップは500nmで製造されていた。各企業は45nmや30nm、さらにそれ以下の細かさのチップを製造するために起こる複雑な技術的課題を解決するため、ナノテクノロジーを用いて開発を行っている。これらのプロセス技術は半導体産業が直面するムーアの法則の限界を延命させるだろう。
最近のコンピュータ業界の技術ロードマップ（2001年）は、ムーアの法則はチップ数世代にわたって継続するであろう、と予測している。この技術ロードマップでの計算によると、この10年間でチップ上のトランジスタ数は2の100乗個にまで増加するだろう。半導体産業の技術ロードマップではマイクロプロセッサのトランジスタ数は3年で2倍になるとしているので、それに従うと10年で2の9乗個になる。
2006年初頭、IBMの研究者らは深紫外光 (DUV、193nm) のフォトリソグラフィ技術を用いて、29.9nm幅の回路をプリントする技術を開発したと発表した。IBMは、この技術によってチップ市場は今までのやり方でムーアの法則の予言をこの数年達成し続けることができるだろう、としている。より小さな回路を形成する新手法は、実質より高くつくと予測されている。
計算能力を向上させる方法は、単一の命令ストリームを1つの演算部で可能な限り早く処理するだけとは限らず、遅い動作クロックであっても複数の演算部で並列的に処理することでも計算能力を向上できる。一般に動作クロックの上昇は処理性能に寄与するが、発熱もまた増すために、ある程度まで高速化された演算部では処理性能の向上よりも発熱量の増加が上回り、高集積な回路であれば放熱問題に直面して、動作クロックの高速化は現実的でなくなる[5]。
ムーアの法則を基にして、ヴァーナー・ヴィンジやブルース・スターリング、レイ・カーツワイルのような有識者が技術的特異点を部分的に推定している。しかしながら、2005年4月13日、ゴードン・ムーア自身が、「ムーアの法則は長くは続かないだろう。なぜなら、トランジスタが原子レベルにまで小さくなり限界に達するからである」とインタビューで述べている。
（トランジスタの）サイズに関して、我々は基本的な障壁である原子のサイズに到達するであろう。しかし、その向こう側に行くにはまだ2, 3世代ある。そして、我々が見ることができるよりもさらに向こう側がある。我々が基本的な限界に到達するまでにはあと10〜20年ある。そのときまでには10億を超えるトランジスタを搭載するより巨大なチップを作ることができるだろう[6]。(2005年の発言）
ムーアの法則を今後も時間軸に沿って維持するには、裏に潜む様々な技術的挑戦なしにはなしえない。集積回路における主要な挑戦のうちの一つは、ナノスケールのトランジスタを用いることで増加する特性のばらつきとリーク電流である。ばらつきとリーク電流の結果、予測可能な設計マージンはより厳しく、加えてスイッチングしていないにもかかわらず、かなりの電力を消費してしまう。リーク電力を削減するように適応的かつ統計的に設計すると、CMOSのサイズを縮小するのには非常に困難である。これらの話題は「Leakage in Nanometer CMOS Technologies」によく取り上げられている。サイズを縮小する際に生じる技術的挑戦には以下のものがある。
- トランジスタ内の寄生抵抗および容量の制御
- 電気配線の抵抗および容量の削減
- ON/OFFの挙動を制御するためにゲートを終端できる適切なトランジスタ電気的特性の維持
- 線端の粗さによる影響の増加
- ドーピングによる変動
- システムレベルでの電力配送
- 電力配送における損失を効果的に制御する熱設計
- システム全体における製造コストを常に引き下げるようなあらゆる技術的挑戦
カーツワイルの目算は、ムーアの法則が2019年まで継続することにより、将来たった原子2, 3個分にしかない幅のトランジスタがもたらされるというものである。もちろん、より高精度なフォトリソグラフィーを用いるやり方によって達成できるが、このことはムーアの法則の終わりを意味するものではないと彼は考えている。
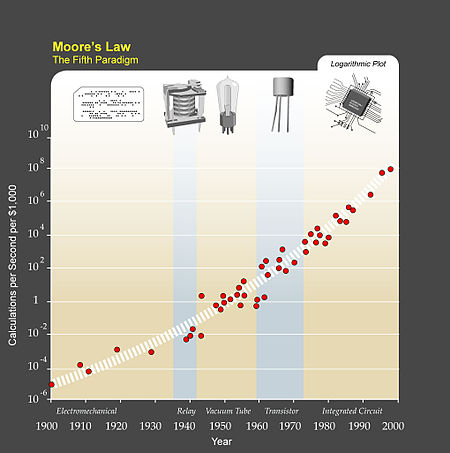
集積回路におけるムーアの法則は、価格対効果を加速する最初のではなく5番目のパラダイムである。コンピュータは(単位時間当たりの)処理能力はずっとに何倍にもなってきた。1890年にアメリカの国勢調査で使用された機械式計算機器からLorenz暗号を破るためのMax Newmanのリレー式計算機"Robinson"、アイゼンハワーの選挙予想に使われたCBSの真空管式コンピュータ、最初の宇宙旅行に使われたトランジスタ式のコンピュータ、集積回路を用いたPCへと[7]。
カーツワイルは、なんらかの新しい技術が現在の集積回路技術を置き換え、ムーアの法則は2020年以降もずっと長く維持されるのではないか、と推測している。彼は、ムーアの法則の指数関数的な成長は、技術的特異点をもたらすであろう集積回路の技術への適用を超えて、今後も続くであろうと信じている。「収穫加速の法則」の中でカーツワイルは、多くの方法によってムーアの法則の一般的な認識は変更されてきたと述べている。ムーアの法則は技術のすべての形を予測すると共通に(しかしそれは誤っているが)信じられている。たとえそれが実際には半導体回路に関してのみ適用されるものとしてもである。多くの未来学者は、いまだカーツワイルによって力を与えられたこれらの考えを述べるために、「ムーアの法則」という言葉を用いている。
KraussとStarkmanは彼らの論文である「Universal Limits of Computation」で、宇宙に存在するあらゆるシステムの情報処理容量の合計を厳密に見積もった結果、600年という非常に長い期間をムーアの法則の限界と発表した。
この法則は明らかに克服できないように見える障害にしばしば直面したが、すぐにこれらを乗り越えていった。ムーア氏は、自分が実現した以上に今やこの法則が美しいものに見える、と述べている。「ムーアの法則はマーフィーの法則に違反している。すべてのものはどんどんよくなっていくのだ。」[8]
他の関心事 [編集]
コンピュータ技術において、ムーアの法則に従って開発が進むのは容量と速度だけではない。RAMの速度とハードディスクのシークタイムは最高年2, 3％ずつ改善されている。RAMとハードディスクの容量はそれらの速度と比べて非常に速く増えているので、それらの容量をうまく使うことはますます重要になっている。多くの場合、処理時間とスペースは交換できることがわかっているので、素早いアクセスを行うためになんらかしらの方法で処理前にインデックスをつけてデータを格納しておく方法などである。コストの点で、より多くのディスクやメモリのスペースが使われる。スペースは時間と比べてより安くなっている。
他方、時々間違えてしまうが、指数関数的なハードウェアの改良は、必ずしもそれと同様な指数関数的なソフトウェアの改良を意味するものではないということである。ソフトウェア開発者の生産性はハードウェアでの進化と共に指数関数的に確実に増えているというわけではなく、たいていの測定では、ゆっくりとまた断続的に増えていく。ソフトウェアは時間と共により大きく複雑になっていく。ヴィルトの法則では「ソフトウェアは、ハードウェアが高速化するより急速に低速化する。」とさえ述べている。
さらに、もっとも有名な間違った考えは、メガヘルツ神話として知られる、プロセッサのクロック速度が処理速度を決定する、というものである。これは実際には、単位時間当たりに処理できる命令数にも依存するので(それぞれの命令の複雑さも同様に依存する)、クロック速度は単に2つの同一の回路同士を比較する時にのみ用いることができる。もちろん、バス幅や周辺回路の速度のような他の要因も考慮に入れなければならない。それゆえに、もっとも有名な「コンピュータの速度」の評価は、基礎技術を理解しなければ元々バイアスがかかっている。これは特にPentiumの時代には真実であった。この時は有名なメーカーが速度の普通の認識として、新製品のクロック速度を宣伝するのに力を入れていた[9]。
コンピュータの能力を使用する消費者が負担するコストが落ちているが、ムーアの法則を達成するためのメーカーのコストは逆のトレンドをたどっている。研究開発や製造、テストのコストはチップの世代が新しくなるごとに着実に増えている。半導体メーカーの設備にかかるコストも増え続けると思われるので、メーカーはよりたくさんより大きくて利益の出るチップを売らなければならない。(180nmのチップをテープアウトするのにかかるコストは約30万ドルであった。90nmのチップをテープアウトするのにかかるコストは75万ドルを超え、65nmでは100万ドルを超えると思われる。）近年、アナリストたちは先進的なプロセス(0.13umやそれ以下)で「設計開始」された数が減っているのを目の当たりにしている。2000年以降の景気の低迷の間これらのことが観察されたが、開発の衰退は、長い間世界市場にいた伝統的な半導体メーカーが、経営的にムーアの法則を維持できなくなっていることの証拠であるかもしれない。
しかし、2005年のインテルの報告書では、経営的に安定させながらシリコンチップをダウンサイジングすることは次の十年可能である、としている[10]。シリコン以外の材料を使用することが増えるとのインテルの予想は2006年中ごろには確かめられ、2009年までにはトライ・ゲート・トランジスタを使用するつもりであるとしている。IBMとジョージア工科大学の研究者らは、ヘリウムで極低温まで冷却したシリコン／ゲルマニウムチップを500GHzで動作させ、新しい動作記録速度を作った[11]。チップは4.5K(摂氏マイナス268.65度)で500GHz以上で動作し[12]、シミュレーションの結果では恐らく1THz(1000GHz)で動作することも可能であるとしている。
0 件のコメント:
コメントを投稿