ニュートン力学(ニュートンりきがく、英語: Newtonian mechanics)は、アイザック・ニュートンが、運動の法則を基礎として構築した、力学の体系のことである[1]。 「ニュートン力学」という表現は、アインシュタインの相対性理論、あるいは量子力学などと対比して用いられる[1]。
静止物体に働く力の釣り合いを扱う静力学は、ギリシア時代からの長い年月の積み重ねにより、すでにかなりの知識が蓄積されていた[1]。ニュートン力学の偉大さは、物体の運動について調べる動力学を確立したところにある[1]。
ニュートン力学は古典物理学の不可欠の一角を成している。「絶対時間」と「絶対空間」を前提とした上で、3 つの運動の法則(運動の第1法則、第2法則、第3法則)と、万有引力の法則を代表とする二体間の遠隔作用として働く力を基礎とした体系である。広範の力学現象を演繹的かつ統一的に説明し得る体系となっている。
ニュートン力学は、1687年のニュートン自身による、3巻から成る著作『自然哲学の数学的諸原理』(略称: プリンキピア、Principia)を通して公表された[1]。ニュートン力学の主要な点はすべてこの中に含まれていると言ってもよい[1]。
静止物体に働く力の釣り合いを扱う静力学は、ギリシア時代からの長い年月の積み重ねにより、すでにかなりの知識が蓄積されていた[1]。ニュートン力学の偉大さは、物体の運動について調べる動力学を確立したところにある[1]。
ニュートン力学は古典物理学の不可欠の一角を成している。「絶対時間」と「絶対空間」を前提とした上で、3 つの運動の法則(運動の第1法則、第2法則、第3法則)と、万有引力の法則を代表とする二体間の遠隔作用として働く力を基礎とした体系である。広範の力学現象を演繹的かつ統一的に説明し得る体系となっている。
ニュートン力学は、1687年のニュートン自身による、3巻から成る著作『自然哲学の数学的諸原理』(略称: プリンキピア、Principia)を通して公表された[1]。ニュートン力学の主要な点はすべてこの中に含まれていると言ってもよい[1]。
ニュートン力学は、物体を「重心に全質量が集中し大きさをもたない質点」とみなし、その質点の運動に関する性質を法則化し、以下の運動の3法則を提唱した[3][注釈 1]。また、これらの法則は、質点とは見なせない物体(剛体、弾性体、流体などの連続体)に対しても基礎となる考え方である[4][5]。
- 第3法則(作用・反作用の法則)[8][注釈 5]
- 二つの質点 1, 2 の間に相互に力が働くとき、質点 2 から質点 1 に作用する力
 と、質点 1 から質点 2 に作用する力
と、質点 1 から質点 2 に作用する力  は、大きさが等しく、逆向きである。
は、大きさが等しく、逆向きである。
力学分野における数多くの法則や定理は、基本的には、上の三つの法則から導出されるものである。 また、位置ベクトルの時間に対する 2 階の常微分方程式である運動方程式は、ある時刻の位置と運動量(あるいは速度)を与えれば、あらゆる時刻の運動状態が確定する方程式であり、その意味で、ニュートン力学は決定論的であるとされる。
ニュートンの力学は、その後、ダニエル・ベルヌーイ、レオンハルト・オイラー、ピエール・ルイ・モーペルテュイ、ジャン・ル・ロン・ダランベール、ジョゼフ=ルイ・ラグランジュ、ピエール=シモン・ラプラス、ガスパール=ギュスターヴ・コリオリらによって、今日的な力学体系の形にまとめ直され、ラグランジュやウィリアム・ローワン・ハミルトンによる解析力学へと発展した。
電磁気学が19世紀に発展した結果、電磁気学とニュートン力学が互いに矛盾することが問題となった。電磁気学における基本方程式であるマクスウェル方程式は、ニュートン力学における運動方程式と異なり、ガリレイ変換に対する普遍性を持たず、慣性系によらず電磁気学の法則が成り立つならばそれは相対性原理を修正することになる。逆に、ニュートン力学とガリレイの相対性原理が正しいならば、マクスウェル方程式は一般の慣性系では成り立たず、電磁気学を修正する必要がある。
19世紀末から20世紀初頭にかけて、ハインリッヒ・ヘルツ、ジョージ・フィッツジェラルド、ヘンドリック・ローレンツ、アルベルト・アインシュタインらの仕事によって、マクスウェルの理論の正当性が検証され、ニュートン力学は修正されることになる。 修正された新しい力学は特殊相対性理論と呼ばれ、ガリレイの相対性原理ではなくアインシュタインの相対性原理を基礎とし、ローレンツ変換に対して普遍な力学である。
その後に発展した一般相対性理論までの完成された力学は「古典力学」と呼ばれ、1920年代に成立した量子力学と区別される。 量子力学では局所実在論が成立せず、その意味でニュートン力学などの古典論とは決定的に異なっている。

 は、そのとき質点に作用する
は、そのとき質点に作用する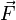 に比例し、質点の
に比例し、質点の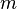 に反比例する
に反比例する

0 件のコメント:
コメントを投稿